q-learning and sarsa
我的理解:
q-learning 在学习的时候,只考虑下一步是不是最优的,即:我是否可以将价值最大化,而不考虑这一步有可能的代价
而sarsa 在学习的时候,不仅考虑下一步是不是最优的,而且考虑代价
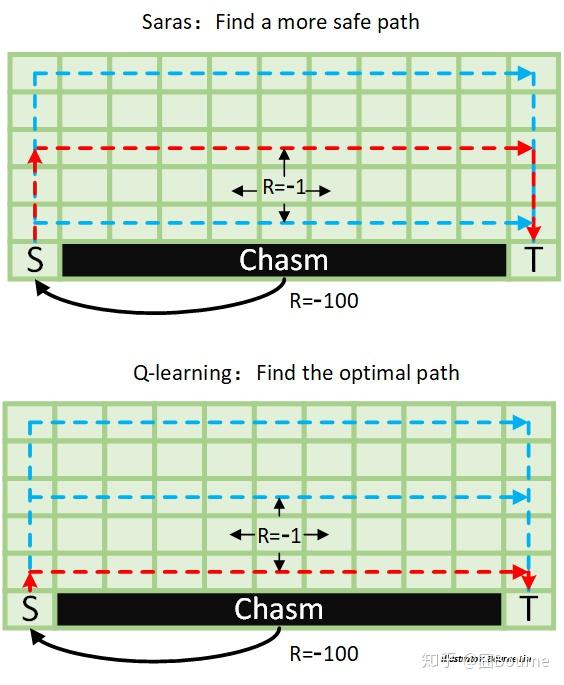
如此图,Qlearning不会顾及下面是悬崖,只知道这样走奖励最大
下文由 简悦 SimpRead 转码, 原文地址 zhuanlan.zhihu.com
为了理清强化学习中最经典、最基础的算法——Q-learning,根据 ADEPT 的学习规律(Analogy / Diagram / Example / Plain / Technical Definition),本文努力用直观理解、数学方法、图形表达、简单例子和文字解释来展现其精髓之处。区别于众多 Q-learning 讲解中的伪代码流程图,本文将提供可视化的算法流程图帮助大家学习、对比 Q-learning 与 Sarsa。
( 在此假设大家已了解 TD Method, ε-greedy policy,off-policy 和 on-policy 相关知识。想了解的童鞋也可在本文最后 Reference 或链接中学习)
一、直观理解
任何强化学习的问题都需要兼顾探索(Exploration)和利用(Exploitation),因此 TD 方法也对应有两种经典的衍生算法:Q-learning(off-policy)和 Sarsa(on-policy)。基于 off-policy 思想的 Q-learning,与 Monte Carlo 方法中 off-policy 的灵魂思路是一致的,除了更新价值的步数不一样之外。在此引用笔者之前回答中关于 off-policy 的一个比喻。
古时候,优秀的皇帝都秉持着“水能载舟 亦能覆舟”的思想,希望能多了解民间百姓的生活。皇帝可以选择通过微服出巡,亲自下凡了解百姓生活(On-policy),虽然眼见为实,但毕竟皇帝本人分身乏术,掌握情况不全;因此也可以派多个官员去了解情况,而皇帝本人则躺在酒池肉林里收听百官情报即可(Off-policy)。
(坏皇帝则派出“锦衣卫”_(´ཀ`」 ∠)_)
不清楚 off-policy 的同学可以点击以下传送门:
疑难点在于:对于 Q-learning(off-policy),我们用来产生与环境互动的行为策略,既然其产生的样本数据是用来训练目标策略的,那为什么学习策略可以在某一程度上独立于行为策略呢?这就是一个细节处理问题,因此下面将一步一步剖析这种独立是如何产生。
二、算法流程
本文首先放出两张一目了然的流程图: Q-learning 和 Sarsa,为了可以直接于可视化流程图的比较之中领悟这两种方法的思路和差别。
1. Sarsa
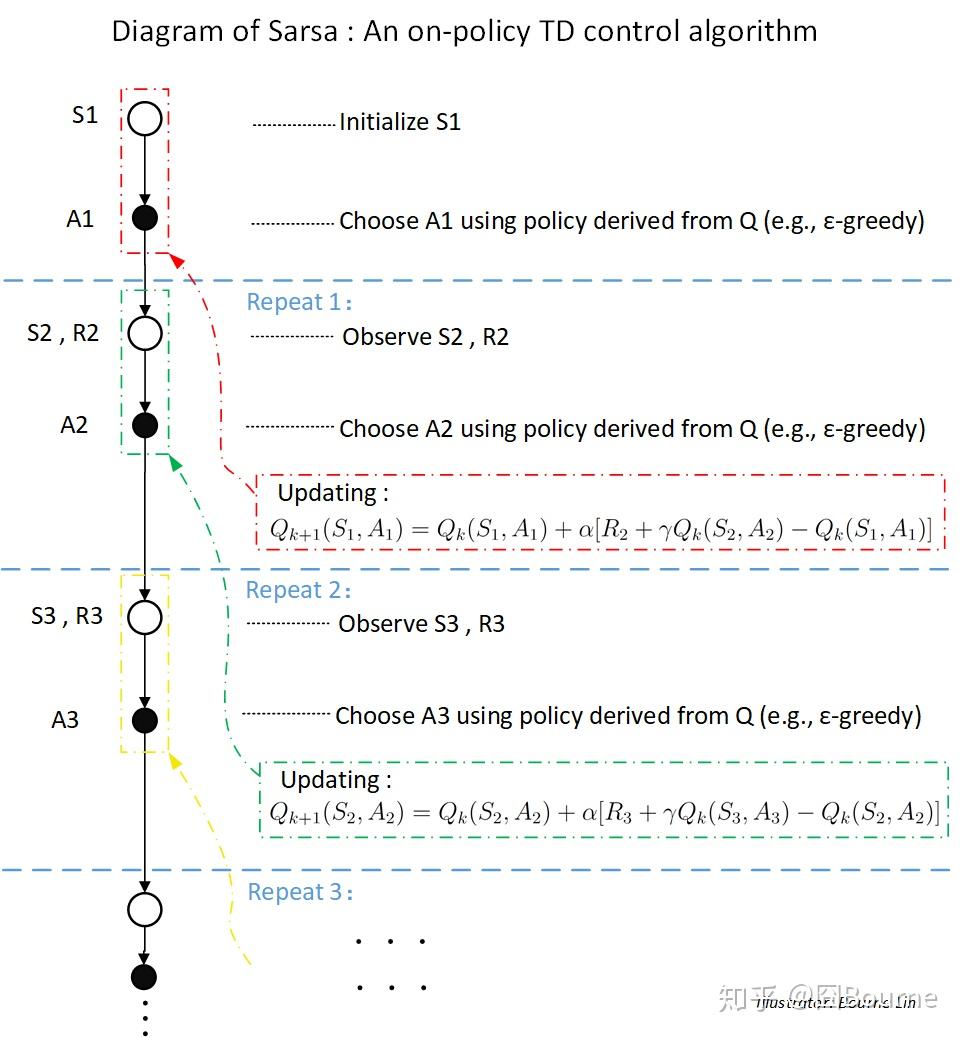
(已了解 Sarsa 的同学也不要轻易跳过,或者对比过后,你会有新的发现)
1.1) 一个回合(Episode)开始,随机选择(初始化)第一个状态
1.2) 进入第一次循环 (Repeat 1 / Step 1):执行
1.3) 不断循环第二步,直到终止状态。
2. Q-learning (也称为 SarasMax)
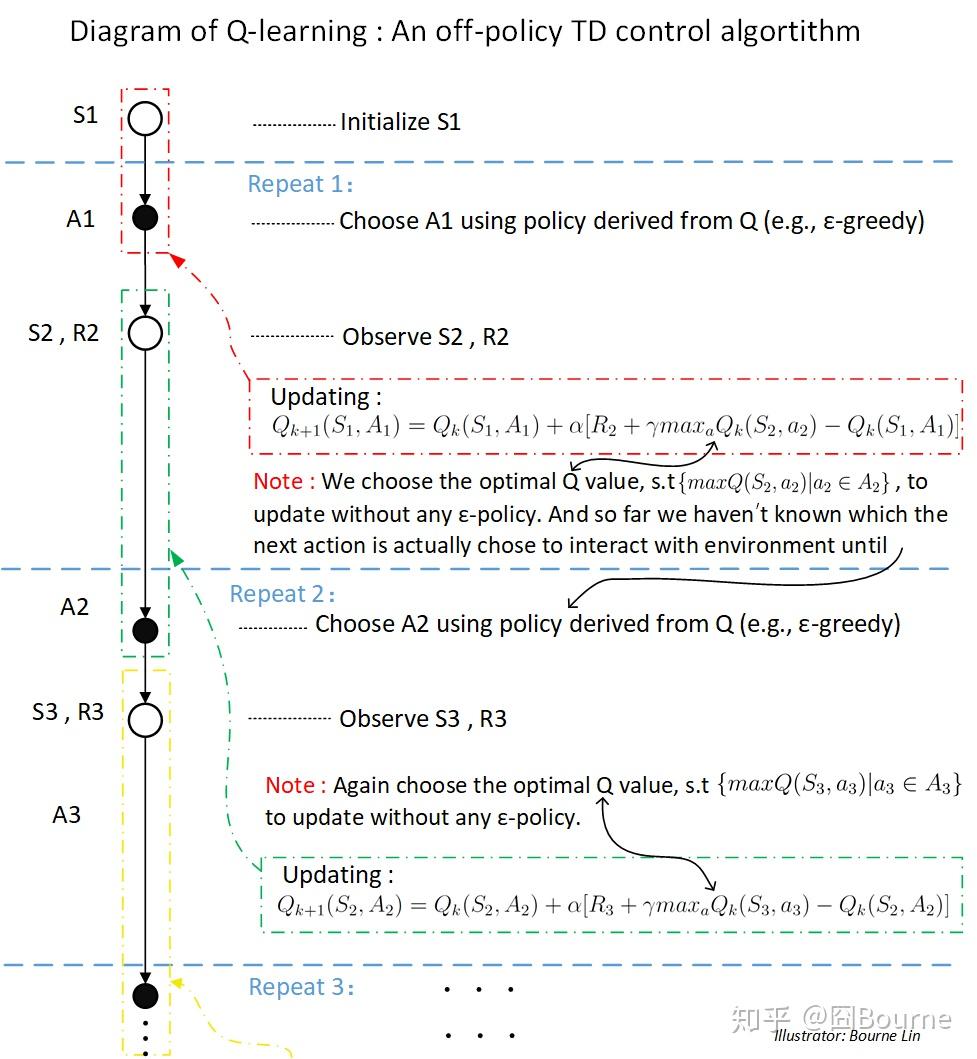
2.1) 一个回合(Episode)开始,随机选择(初始化)第一个状态
2.2) 进入第一次循环(Repeat 1 / Step 1):首先基于 ε-greedy 策略在状态
2.3) 更新完毕后,进入第二次循环:基于 ε-greedy 策略,在状态
- 细节
不少学童鞋对这两幅伪码图中的动作符号存疑:为什么动作的表示有时候为大写的 A,有时候为小写的 a?
(引用 R. S. Sutton 与 A.G. Barto 于 2018 年 1 月 1 日发布的《Reinforcement learning: An introduction》第二版):


大写的 A 表示集合,比如
此时我们可以清楚知道 Sutton 书中的伪代码的全部含义啦 ^_^!
三、Q-learning 如何实现更加有效的探索?
清楚整个流程之后,我们来具体看看,Q-learning 到底是怎么实现有意义的探索,如何在环境中发掘出更有价值的动作?(即一个当前估值(evaluate)不高但潜力巨大的动作的逆袭之路)
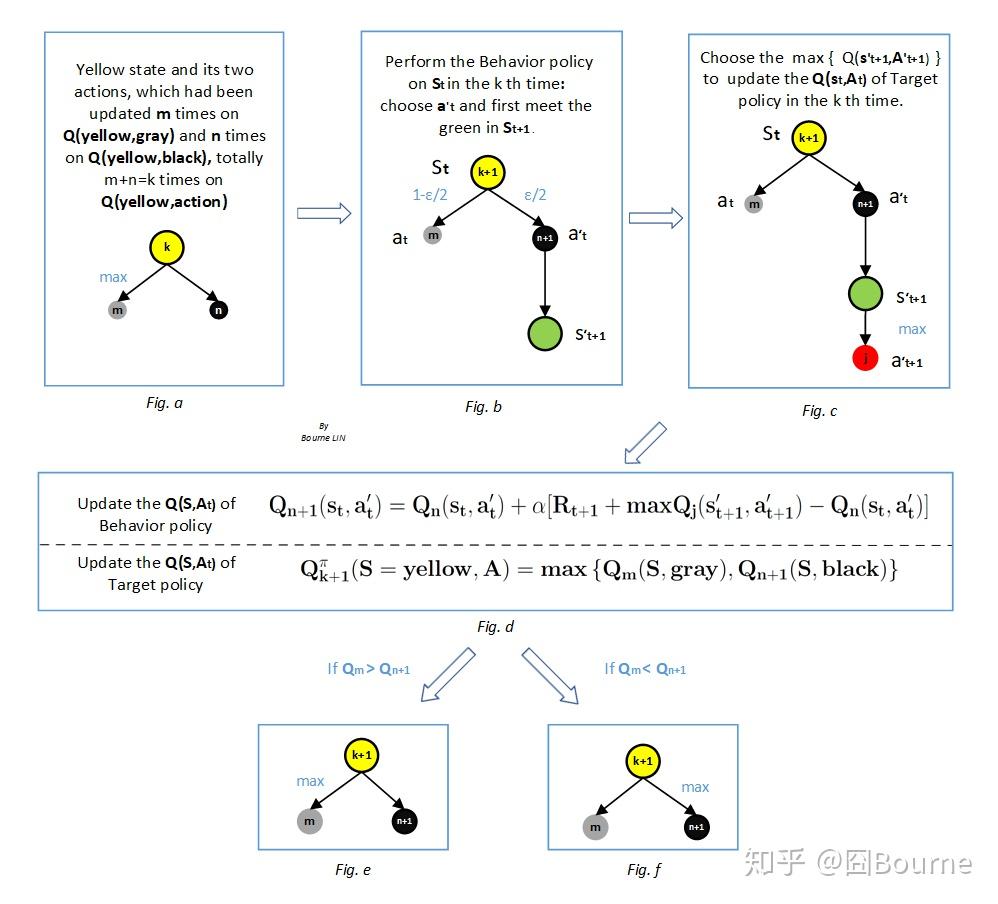
在这个例子中,我们将更新黄色状态的动作价值
图 a,假设已知黄色状态下只有两个动作可选:灰动作和黑动作,并且在第 k-1 次更新
Q{n}(yellow,black )">$Q{m}(yellow,gray)>Q{n}(yellow,black )$Q{m}(yellow,gray)>Q_{n}(yellow,black )
其中 m,n 为对应动作价值已迭代更新的次数,k 为
图 b,在某个回合(episode)中,在时间步为 t 的时候(time step = t),所处状态为黄色,又已知灰动作价值比黑动作大,即基于 ε-greedy 的行为策略选择动作,会出现情况①或②:
① 有
而另一黑动作没有更新。
其中,
② 有
而另一灰动作没有更新
其中,
在此假设图 b 发生②的情况,则
图 c 通过选取
在第 k+1 次更新中,我们通过取最大值(即 greedy 思想),选取 Q 值最大的动作来更新目标策略
比如,基于上述已发生的,再发生图 f 的情况,则在下一次更新
(实际上无论发生情况①或是②,黄色状态下的灰动作与黑动作的价值的大小关系都可能发生变化!!)
四、另一个栗子
在此举一个非常直观的例子来帮助我们认识一下 Q-learning 和 Sarsa 的实际应用效果的区别。
在下面栅格化的小世界中,绿色区域为草地,在上面每移动一格子就会扣 1 分,而踏入黑色区域的悬崖(chasm),会扣一百分,并且回到起始点 S (Start)。我们希望能学习到一条得分最高的路径到达终点 T (Terminal)。分别使用 Sarsa 和 Q-learning 进行学习。结果如图所示,红色为相应算法的最优路径。

可以看到,Q-learning 寻找到一条全局最优的路径,因为虽然 Q-learning 的行为策略(behavior)是基于 ε-greedy 策略,但其目标策略(target policy)只考虑最优行为;而 Sarsa 只能找到一条次优路径,这条路径在直观上更加安全,这是因为 Sarsa(其目标策略和行为策略为同一策略)考虑了所有动作的可能性( ε-greedy),当靠近悬崖时,由于会有一定概率选择往悬崖走一步,从而使得这些悬崖边路的价值更低。
五、总结
Q-learning 虽然具有学习到全局最优的能力,但是其收敛慢;而 Sarsa 虽然学习效果不如 Q-learning,但是其收敛快,直观简单。因此,对于不同的问题,我们需要有所斟酌。
Reference
- Watkins C J C H, Dayan P. Technical Note: Q-Learning[J]. Machine Learning, 8(3-4):279-292, 1992.
- R. S. Sutton and A. G. Barto. Reinforcement learning: An introduction. IEEE Transactions on Neural Networks, 9(5):1054–1054, 2018.
声明:本图文未经作者允许,谢绝转载。